hwakのトリビアルな雑記集

初めまして、個人研究者のhwakです。個人的に量子アルゴリズムの研究をしております。

Re:ゼロから始める量子多クラス分類

この記事は、量子サポートベクターマシーンを利用して、MNISTから配布されているデータベースの分類を行う方法をある程度略して説明するものです。変分量子計算の方法論は、機械学習における分類問題にも応用されています。その1つがQuantum Support Vector Machine(QSVM)です[1]。これはクラス分類問題において、評価関数に現れるカーネルを量子状態の内積で代用して、それを解くというものです。この方法において、過学習が抑えられるということが報告されています。本来ならば、実装してデータを採りたいところですが、手書き文字の認識分類をさせるだけでも画像を取り込んだ上に数字とアルファベットの全36種類の分類を行わなければならないため、私のパソコン環境では実装出来ないと判断しました。そのため、理論の話にとどめます。まずはタイトル通り、機械学習における2クラス分類の基礎から説明します。

機械学習の基礎:

機械学習の基本は、与えられたデータ \mathbf{x} に対するクラス分類を行うことです。もっとも簡単な例はn次元平面上における一次関数における評価関数の値の範囲の中に有るか無いかを判定する問題です。入力するデータを \mathbf{x} として式で表せば、

0 = \textbf{ w }^\dagger \textbf{x } + b \tag{1}

となります。分類のうちどちらかを表す空間 C \in { +1, -1 }、i番目の入力データに対応するその分類を表す符号変数 y_i \in { +1, -1 }を導入し、 \mathbf{w} のノルムで割りマージンを取ることで、

y_i ( \textbf{ w }^\dagger \textbf{x }_i + b) \geq 1, \quad i \in \{1, 2, \dots, t \} \tag{2}

の関係が導かれます。ここで、 tは入力されるトレーニング用データの数です。こうして、データセット x( \mathbf{w},b) に対する評価関数の結果はかっこの中身の符号を返す関数 \text{sign}()を使って、

m(x( \textbf{ w },b)) = \text{sign}( \textbf{ w }^\dagger \textbf{x } + b) \tag{3}

となります。これは異なる分類に属する距離（マージン)の最も大きい2点間をつなぐサポートベクトルのノルム \mathbf{w} を最小化する問題です。そのため、ラグランジュの未定乗数法と同じ形に表すことができ、

L_p = \frac{1}{2} || \textbf{ w }|| - \sum_{i=1}^{t} \alpha_i y_i ( \textbf{ w }^\dagger \textbf{x }_i + b) + \sum_{i=1}^{t} \alpha_i \tag{4}

となります。

\frac{\partial L_p}{\partial b} = \frac{\partial L_p}{\partial \textbf{ w }} = 0

となるため計算機での処理が可能なように、

L_D = \sum_{i=1}^{t} \alpha_i - \frac{1}{2} \sum_{i,j=1}^{t} \alpha_i \alpha_j y_i y_j \textbf{x }_i^\dagger \textbf{x }_j \tag{5}

と変換できます。この関数は分類数空間を C \in {1, 2, \dots, c }として束縛条件 0 \leq \alpha \leq c、 \sum_{i=1} \alpha_i y_i = 0に従います。この関数はコスト関数と呼ばれる、多クラス分類において最も重要な式です。この関数を最大化する \alphaの組を見つけることでデータセットを正しく分類することがクラス分類の目的です。この中の \textbf{x}_i^\dagger \textbf{x}_j は二値カーネルと呼ばれるもので、 K( \textbf{x }_i, \textbf{x }_j )と表されます。

これを問題の特徴に応じて適切なものを選ぶことで、計算の精度が格段に上がることが知られています[2]。

QSVMにおいては、これは異なるデータセットから作った状態間の内積 |\langle \Phi( \textbf{x }_i) |\Phi( \textbf{x }_j) \rangle|^2 となります。

量子多クラス分類:

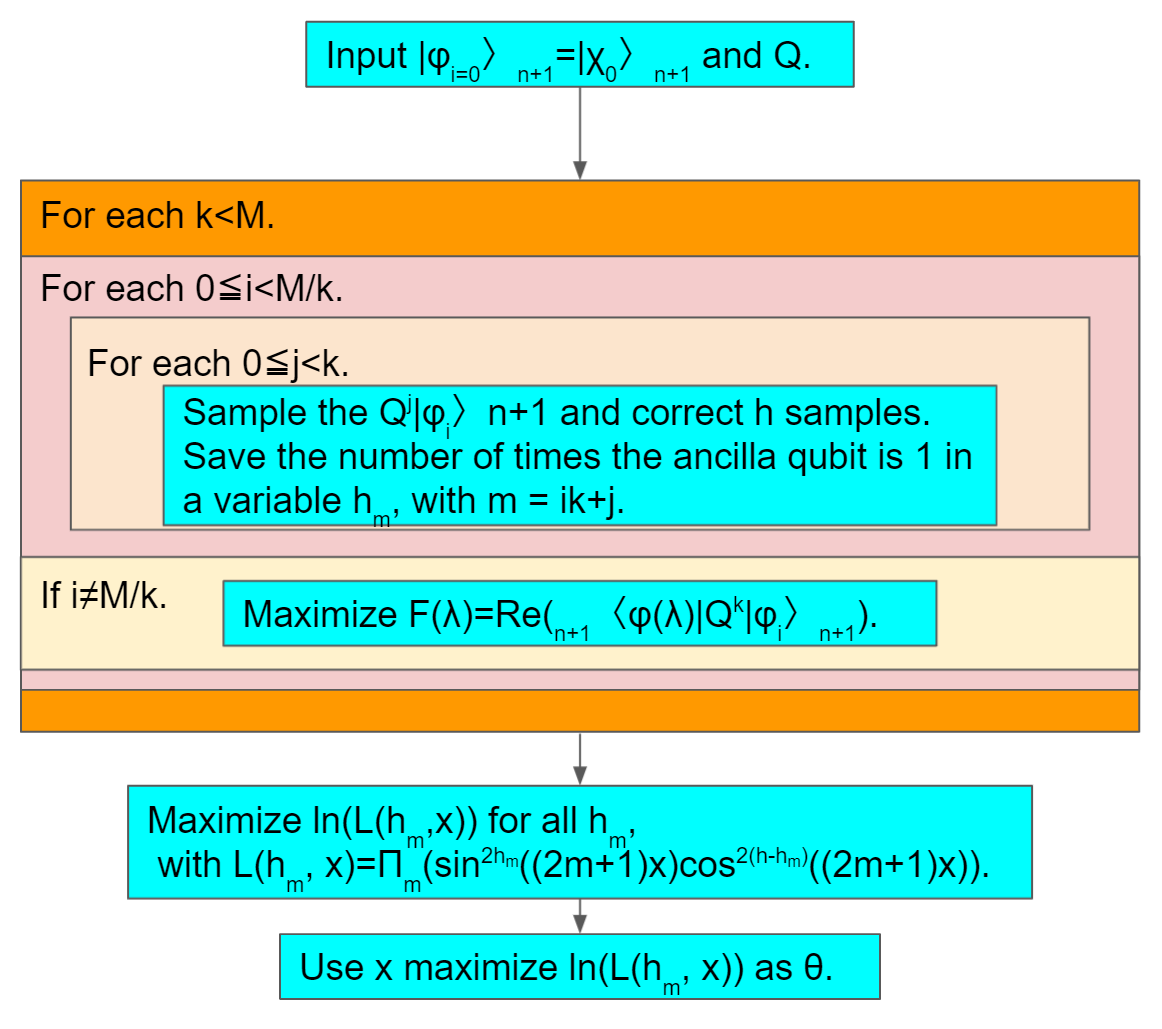
この節では、いよいよ量子多クラス分類の説明をしていきます。多少複雑ですが、それぞれのプロセスで行うことはそれほど複雑ではありません。このアルゴリズムの工程は主に3つです。

  1. 量子多クラス分類機にトレーニング用データセットt子を学習させます。

  2. 式(5)のコスト関数を計算します。

  3. 量子多クラス分類機における1,で最適化された変数θと経験的コスト関数$R _ { emp}$を基に、テストデータセットを分類させます。

1,と3,の大まかな工程を図1,2にそれぞれ示します。

図1 トレーニング用データセットを学習させるプログラムの大まかな流れ。 𝜃 は最適化変数、 𝑊 ( 𝜃 ) はハミルトニアンに相当する量子回路です。

図2 学習した最適化変数と経験的コスト関数を利用して 𝑠 ∈ 𝑆 の分類を行う流れ。

2クラス分類の場合はそれらの図において、

\begin{align*} y \in \{+1, -1\}, \quad f: \{0,1\} \rightarrow \{+1, -1\}, \quad M_y &= \frac{1}{2} \left( I + y \sum_{z \in \{0,1\}^n} f(z) |z\rangle\langle z| \right) \tag{6} \end{align*}

|\Phi( \textbf{x })\rangle を実現する回路は R_z(\theta) ゲート、 exp(i\theta Z_i Z_j) の回路で実装します。 \textbf{ w }(\theta) も同様です。

\begin{align*} p_y( \textbf{x }) &= \langle \Phi( \textbf{x }) | \textbf{ w }^\dagger(\theta) M_y \textbf{ w }(\theta) | \Phi( \textbf{x }) \rangle \tag{7} \\ R_{emp}(\theta) &= \frac{1}{T} \sum_{ \textbf{x } \in T} Pr(m~( \textbf{x }) \neq m( \textbf{x })) \tag{8} \end{align*}

を計算し、経験的コスト関数 R_{emp}(\theta) と変数 \theta を最適化します。 2, は2クラス分類の場合は少々異なり、量子ビット数を n としてパウリゲート P_{ \alpha}, \alpha \in {1,2, \dots,4n } に対して、

\textbf{ w }_\alpha(\theta)= Tr[ \textbf{ w }^\dagger(\theta) f \textbf{ w }(\theta) P_\alpha ] \tag{9}

\Phi_\alpha(\theta) = \langle \Phi( \textbf{x }) | P_\alpha | \Phi( \textbf{x }) \rangle \tag{10}

から、

m( \textbf{x }) = sign\left( \frac{1}{2n} \sum_{\alpha} \textbf{ w }_\alpha(\theta) \Phi_\alpha( \textbf{x }) + b \right)

を量子ビット数 n に対して計算します。また、 m( \textbf{x }_i) = y_i とします。

3,の量子カーネルはSWAP-test[3]で計算し、式(11)を \alpha_j^{ * } , \alpha_j^{ * } とbの連立方程式として解くことで、計算出来ます。多クラス分類の場合は式(6)を、

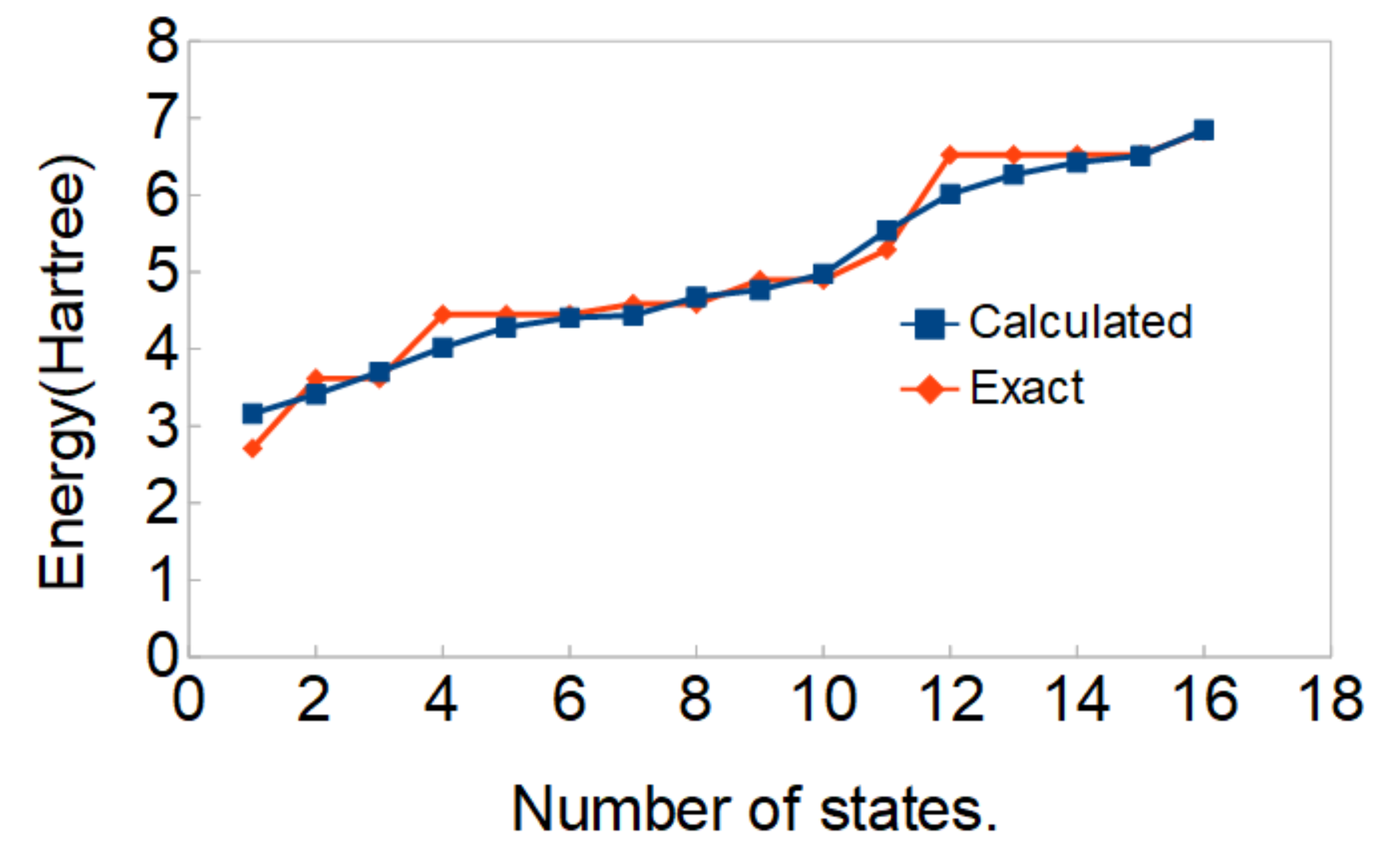
\begin{align*} y \in \{1,2,\dots,c\}, \quad f: \{0,1\} \rightarrow \{+1, -1\}, \quad M_y &= \frac{1}{2} \left( I - \Pi_{i=1}^{log_2 c} g_i y_i \right) \tag{12} \end{align*}

としてあとは1対他あるいは1対1戦略で逐次分類することで図1,2の通りの方法で学習が完了します。 R_{emp} = P_{err} となります。MNISTデータセットも、計算時間と仕様ゲート数は2値分類に比べて大幅に増加しますが、この方法で分類が可能です。

編集後記: 今回は私自身機械学習はタイトル通りゼロから実装を学んだため、非常にざっくりとした説明になってしまいました。もしかしたら、内容に誤りがあるかもしれません。しかしながら、変分量子計算の応用の中で一番難しい部類に入るアルゴリズムの論文を解読し、その内容を分かりやすく説明することは、私にとっても有意義でした。量子機械学習はFault-Tolerant-Quantum-Computer(FTQC)における最有力応用候補として期待されており、更なる発展が期待されています。そしてすでに、量子化学計算においてもクラスターを機械学習で最適化する手法が出ています。なので、私もこれを機に、量子機械学習の研究を始めようと思います。

[1] Vojtech Havlicek, Antonio D. Córcoles, Kristan Temme, Aram W. Harrow, Abhinav Kandala, Jerry M. Chow, Jay M. Gambetta, arxiv, 1804.11326quant-ph

[2] Qiskitで量子SVMを実装して性能評価してみた - Qiita

[3] Juan Carlos Garcia-Escartin and Pedro Chamorro Posada, arxiv, 1304.4923quant-ph

【PR】初心者も安心のサポート充実【DMM FX】

楽天Kobo

反復量子位相推定アルゴリズム【実践編】

アルゴリズム

今回は、前回「反復量子位相推定アルゴリズム by Hikaru Wakaura 」に引き続き、反復量子位相推定[1]における実際の計算を行う際の注意点を説明し、実践した結果を示します。

事前に、固有値を求めるハミルトニアンにおける固有値の最大値と最小値の差 D=E_{max}-E_{min} をとります。

今回は CU ゲートの実装には図1の回路を利用します。

\theta の値はHの固有値を規格化するため、各項の係数をcとして - c ^2 \pi / D とします。

実際の計算では、 CU ゲートとともに固有値の定数シフトを行うための制御位相ゲートを角度 2\pi(E_{min}-e)/ D として全計算用ビットを標的ビット、アンシラビットを制御ビットとして掛けます。

ここで、 eはハミルトニアンHの定数項部分です。これも CU を掛けるのとセットで 2^{k-1} 回反復します(図2)。

図1 CU ゲートを実装する回路。U の中身はトロッター展開されたハミルトニアンを指数とする指数関数です。

例えば、 exp(−i \sigma_0 ^x \sigma_1 ^y \sigma_2 ^z ) を掛ける場合、 G_0 は H に、 G_1 は R_x(\pi/2) に、 G_2 は I ゲートになります。

図2 実際の反復量子位相推定アルゴリズムで使用する回路。

この処理によって、基底状態の固有値は \Phi(0)=0 に、最大固有値における状態は \Phi(0)=\Phi_{max} に相当するように調整されます。これによって、固有値が正確に計算できるようになります。計算された蓄積位相から固有値は E=\Phi(0)D+E_{min} となります。今回、水素分子における基底状態を反復量子位相推定を用いて計算しました。原子間距離は0.1から2.5 Å まで0.1刻みで計算し、位相は 1/\sqrt{2^{11}} の桁まで取り、回路深さは1としました。その結果を図3に示します。

r\lt 1.0 の領域においては厳密解とほぼ一致していますが、それ以上の原子間距離では厳密解から少し離れます。STO-3G基底における厳密解を E_{FCI} とした場合におけるエラー量の対数 (Log error) \log_{10} |(E-E_{FCI})/E_{FCI}| も同様に、 r\lt 1.0 の領域では小さくなっており、精度は理論と少し違い、化学精度 (エラー量の対数 -2.8以下) のだいぶ上でした (図4)。 r=0.9 においては完全に化学精度を超えています。 r\gt 1.5 の領域におけるエラー量の大きさは他の状態との間の縮退の影響と考えられます。また、VQE法においてハミルトニアンを深さ2の回路で最適化して固有状態を計算したためであると推察されます。

図3 反復量子位相推定アルゴリズムで計算した基底状態のエネルギーと水素原子間距離の関係。

図4 反復量子位相推定アルゴリズムで計算した基底状態のエネルギーのエラー量の対数と水素原子間距離の関係。

図5に$t=11$とした場合における反復回数に対する基底状態における原子間距離 r=0.9 の場合の計算されたエネルギーと厳密解との差、 \Phi(k) の変化を示します。 k\lt 4 の領域ではアンシラが1の場合状態における存在確率がわずかに高くなり、そちらが出てしまいますがそれ以降はすべて0となり、最終的には化学精度を超えます。

量子位相推定アルゴリズムと同様に、精度を上げるには指数オーダーで計算量を増やさなければならないのは同じですが、こちらはゲートの印加回数が増大するのみで済みます。励起状態の計算手法を相当工夫しなければ、そちらを求めることは出来ないなど課題は多いですが、将来有望な誤り耐性アルゴリズムです。

図5 t-kの増大に対する計算された基底状態エネルギーとその厳密解の差と \Phi(k) の変化。

[1] M. Dobsicek, G. Johansson, V.S. Shumeiko, G. Wendin, arXiv[quant-ph], 0610214v3(2007)

【PR】初心者も安心のサポート充実【DMM FX】

楽天Kobo

反復量子位相推定アルゴリズム

アルゴリズム

今回は、反復量子位相推定アルゴリズムの説明をします。Abrams氏とLloyd教授による量子位相推定の量子計算への応用可能性が示唆されてから8年後にGoranらによってより高速に計算できるようにこの方法が考案されました。このアルゴリズムは、量子位相推定における位相に対応する固有状態の情報をとれない代わりに、固有値を高速で求めることが可能です[1]。但し、こちらの方は一度にとれる固有値は全部の中から初期状態とする状態に一番近い1つのみが選ばれます。

このアルゴリズムにおける流れは次の通りです。

今回、 R_z ( \theta ) = exp ( − i \theta / 2 ) ∣0⟩⟨0∣ + exp ( i \theta / 2 ) ∣1⟩⟨1∣ としています。

1, 1アンシラビット、計算用ビットをnビット用意します。蓄積位相の初期値はΦ(k=t)=0 です。

2, アンシラビットにHと R_z    ( 2 \pi \Phi ( k ) ) を掛けます。

3, アンシラビットを制御ビットとして C U を 2^{ k - 1 }   回掛けます。

4, アンシラビットにHを掛けます。その後アンシラビットが1であれば蓄積位相Φ(k)にΦ(k−1)=Φ(k)/2−1 とします。

5, 2-4をkが0になるまで繰り返します。

6, 固有値がexpの位相2πΦ(0) として出てきます。

詳しい流れは図1にも示しました。蓄積位相は二進小数で表されます。それについてはご存じない方は「量子フーリエ変換【ソース公開有】」を参照してください。このアルゴリズムはhttps://dojo.qulacs.org/ja/latest/notebooks/7.1_quantum_phase_estimation_detailed.html#%E5%8F%8D%E5%BE%A9%E7%9A%84%E4%BD%8D%E7%9B%B8%E6%8E%A8%E5%AE%9Aを参考に組みましたが、Qulacsとblueqatでは勝手が違い、大筋は同じですが変数はこちらの方でないと正しく動きません。回路自体は、やっていること自体は簡単ですが、実際の計算ではいくつかのテクニックが要求されます。

固有値を[0,2π] の範囲に入るように規格化し、定数シフトを行わなければなりません。

それは次回説明します。

図1 反復量子位相推定において使用する回路。

[1] M. Dobsicek, G. Johansson, V.S. Shumeiko, G. Wendin, arXiv[quant-ph], 0610214v3(2007)

【PR】初心者も安心のサポート充実【DMM FX】

楽天Kobo

論文紹介:ノイズ耐性のあるブラインド量子計算

論文紹介

今回はブラインド量子計算をノイズに耐性を持たせて行う研究を紹介します。この論文における要点は次の通りです。

 

・光ファイバーにおける伝送ノイズに強いブラインド量子計算を実現するものです。

・ビームスプリッターを組み合わせて’ノイズプロセッシング’を行うことでノイズを抑えます。

・ノイズ耐性がそれで向上しました。

 

この研究は量子通信、特に計算内容を秘匿しつつその結果を通信するブラインド量子計算のものです。ノイズを不完全ビームスプリッターで作り、その周りにノイズプロセッシング回路を作り、そこにTime-bin状態に搬送する量子情報を載せたものを初期状態として投入します。そのプロセスは次の通りです。

 

1、アリスが状態 を用意します。

2,アリスが状態をエンコードします。

3,アリスはボブに量子状態を送りますが、途中でノイズにさらされます。

4,ボブはノイズによってデータが損失した量子状態を受け取ります。

5,不完全ビームスプリッタを含むノイズプロセッシング回路を用いて受け取った量子状態をデコードします。

6,ボブはグラフ状態を作り、それの内j番目の量子ビットを観測します。

7,ボブは観測結果をアリスに報告し、その結果に基づいてアリスは計算を完了します。

 

ノイズをノイズを意図的に発生させることで相殺し、ブラインド量子計算を実現することで、ノイズ発生を抑えるのは逆転の発想と言えるでしょうが、ノイズもユニタリー変換によって再現できることを考えればある意味当然です。現在、世界中で家庭用量子計算機を実現する勢いで量子計算機のダウンサイジングが行われています。しかし、現行の技術の延長線上では量子化学計算をそれらで行えるのはまだまだ先です。なので、この結果含めたブラインド量子計算はあと10年程度は廃れずに使われるかもしれません。

 

[1609.08902] Blind quantum computation with noise environment (arxiv.org)

楽天Kobo

論文紹介:固有状態熱化仮説

論文紹介

今回は量子情報熱力学の重要概念である固有状態熱化仮説（ETH)の話をします。これは、量子系における物理量の固有状態におけるトレースは、小正準集団に無限時間後に一致するというものです。これは経験則でありながら非可積分系全般といくつかの可積分系において成り立つことが示された法則です。これは量子エルゴ―ド性、揺らぎの定理にも整合します。非可積分系は量子クエンチが起こることで量子可積分系や局在系になる系が存在し、それを用いて数値実験が行われました。最終ハミルトニアンが長さ21と24になるハードコアボソンとフェルミオンの鎖における1粒子マタギホッピング項、交換相互作用と超交換相互作用がが存在する系における波数モーメントには、明確にサイズが増えることによる揺らぎの減少が見られました。また、超交換相互作用とマタギホッピング項の係数t'=V'と小正準集団における離散周波数kに対する波数の期待値 ⟨𝑛𝑘⟩mc の関係はサイズごとにボソンとフェルミオンで同じ極小値が現れ、温度依存性も確認されました。t'=V'は可積分系である粒子差の可積分性を壊す項なので、これらが0に近づくほど小正準集団における平均期待値が量子力学的期待値から逸れるのは、理論と一致しています。

古典熱統計力学から輸入された経験則ではありますが、これは熱力学と量子力学を結ぶ重要な役割を果たしています。ここから量子情報熱力学へと発展していきます。

[論文リンク](https://arxiv.org/abs/1108.0928)

楽天Kobo

 

 

 

論文紹介:量子モンテカルロの新手法、Variational Quantum Amplitude Estimation

論文紹介

今回は、2021年に出てきた新しい量子モンテカルロ手法であるVariational Quantum Amplitude Estimation(VQAE)の提案論文「[2109.03687] Variational quantum amplitude estimation (arxiv.org)」を紹介します。

 

これは量子モンテカルロ法における計算時間のエラーレートに対する関係を改善するためのものです。量子モンテカルロ法、古典モンテカルロ法とは、特定の関数f(x)≒∑jMcjhjにおける右辺を左辺に近付けるための手法です。通常の量子モンテカルロ法においては計算時間はエラーレートεに対してO(1/ε)となりますが、これはサンプル数Mに対して2M個に分割した場合のものです。しかし、この論文で提案された手法はエラーレートに対してO(1/ε1+β)の精度を発揮し、サンプル数はMです。βは完全な古典モンテカルロに対して1となり、量子の場合には0となる定数です。実際の計算ではその間となります。このモンテカルロ法における最も時間を要する部分はグローバー演算子を複数かける部分です。これを変分計算で再現することで、計算回数を減らしたうえで精度を上げるのが、VQAE法の概要です。その流れは図1に示すものです。後処理のθを最適化する部分はグリッドサーチで5000点に対して行います。

図1 論文で紹介されたVQAEのフローチャート。Qはグローバー演算子です。

 

この手法は私の論文の内容としたFrame Superposition Cluster(FSC)[1]と非常に似通った手法を用いているため、親近感を覚えました。しかしながら、最適化の手法については説明されていない部分もあり、それ次第では量子モンテカルロ以上の時間を要するのではないかとも考えられました。方法は非常に優れているので、そこの説明が追加されればよりよい論文になる事が期待されます。

 

[1][2107.02979] Frame Superposition Cluster: The method to derive the transition matrices in high accuracy (arxiv.org)

楽天Kobo

 

 

量子位相推定・位相からの固有値計算

アルゴリズム

今回は、量子位相推定において、位相から固有値を計算する方法でそれらを計算した結果を示します。

 

「量子位相推定とその注意点 by Hikaru Wakaura 」の方では、Variational Quantum Eigensolver(VQE)法と同様に、固有状態でハミルトニアンを挟んでこれらを計算していました。

 

今回は量子位相推定の初期状態はVQE法で求めた基底状態として、ハミルトニアンの回路深さは1としました。今回は水素分子におけるSTO-3G基底におけるハミルトニアンを使用し、水素原子間距離0.1(Å)の値のみを利用しました。また、今回もアンシラビット数は10、それの観測回数は16回としました。その結果を図1に示します。基底状態を初期状態として、企画課と定数シフトをしたにもかかわらず、初期状態は観測されませんでした。しかしながら、三重項状態、一重項状態、二電子励起状態は所定の精度(厳密解との差は0.01以内)で計算することができました。しかしながら、位相から固有エネルギーを計算する方法は事前に最大、最小値を計算しなければできません。未知系においては、最初に量子位相推定でいきなりエネルギーを計算することは出来ないということです。更に、その求めた値における精度次第では、量子位相推定における最大精度が決まってしまいます。なので、VQEなどほかの手法も残ると考えられます。

図1 水素分子の原子間距離0.1(Å)における計算された結果と厳密解。

楽天Kobo